解析数論と関連分野間の相互関係の解明とその応用

2014年
出典： ソフィアサイテック vol,25

中筋 麻貴（情報理工学科・准教授）

　18 世紀の数学者オイラーは、という形をした多くの無限和の値を計算しました。
　例えば、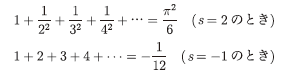
などがその計算結果です。後者の結果を初めて見たとき、非常に驚きましたが、今では普通に思えるようになりました。またオイラーはこれらの計算結果から、 が「対称性」を持つ事を発見しました。その約100 年後、ドイツの数学者リーマンはオイラーの無限和をとおき、を複素変数に拡張したゼータ関数を定義しました。このゼータ関数は素数と関係していることがわかっており、現在でも素数分布の研究をはじめ、解析数論における中心的な研究対象となっています。

　ゼータ関数を一般化したものを複素数列を用いてと表し、これをディリクレ級数と呼びます。が常に1 であればゼータ関数であり、（ディリクレ指標）のとき、ディリクレのL関数と呼ばれる関数になります。ディリクレのL関数は初項と公差が互いに素である等差数列（算術級数）の中の素数分布の研究に使われている関数で、これも「対称性」をもつことが知られています。
　当研究室では、このような「対称性」をもつ特殊な関数に注目し、その性質の解明や応用を目標に研究に取り組んでいます。

　ここでは次の2 つの研究をご紹介します。
［1］多重ディリクレ級数の解明
　多変数に拡張したゼータ関数やディリクレ級数を、それぞれ多重ゼータ関数、多重ディリクレ級数と呼びます。「多重化」の仕方にも色々な定義がありますが、1 変数に比べて、多重化した級数については、どれも多くのことはまだ知られていません。関数等式（対称性）を持たないこともあります。その中で、当研究室では、ワイル群に関係する関数等式を持つ多重ディリクレ級数の性質について研究しています。最近の研究から、この級数が量子群の結晶基底や可解格子模型、シューベルト・カリキュラス（音楽家のシューベルトとは無関係です）といった組合せ論的表現論と呼ばれる分野と関係していることが明らかになってきました。現在は、これをより確実なものとするための研究に取り組んでいます。

［2］スペクトル問題への応用
　ラプラシアンの固有値や閉測地線の長さの分布を用いてゼータ関数やディリクレ級数の幾何学的類似物を構成することができます。当研究室では、このゼータ関数（セルバーグゼータ関数）の性質を解明することで、双曲空間のスペクトルの分布の解明に取り組んでいます。例えば双曲空間のスペクトルには、離散スペクトルと連続スペクトルが存在しており、その存在や分布を解明する「スペクトル問題」があります。これに対し、セルバーグゼータ関数の性質を解明することで、連続スペクトルが離散スペクトルより大きな割合で存在するという結果を得ることができました。さらなる展開として、離散および連続スペクトルのより詳しい分布状況の解明に取り組んでいます。

　当研究室の特長は、解析数論と他分野との相互関係を用いた研究を行うことです。先ほどの例も、［1］解析数論の研究対象と組合せ論的表現論における研究対象との相互関係、［2］解析数論の研究対象と幾何学問題の研究対象との相互関係を用いた研究です。研究を進めるに従い、今後もまた違った分野への展開や応用などが見えてくることと思います。研究室に配属される学生と一緒に、計算、理論、プログラミングなどを通して、解析数論とその関連分野間の相互関係の解明とそれを用いた応用に取り組んでいきたいと思っています。